O básico do básico na dinâmica newtoniana

As 3 leis fundamentais de Newton, no domínio clássico não relativístico com      v <<  c (velocidade muito menor que a velocidade da luz no vacuo, que vale uns 300.000 km/seg).

1ª – Lei da inércia: um corpo permanece em seu estado de repouso ou UM (movimento uniforme sem aceleração) a menos que alguma força seja aplicada sobre ele. A inércia é uma consequência direta da massa dos corpos, massa entendida como quantidade mensurável de matéria sujeita à interação com os outros corpos do Universo (esse é o conceito de massa inercial, que não pode ser confundido com mass gravitacional ou carga gravitacioanal).

2ª – Princípio da ação e reação: a toda ação haverá uma correspondente reação. Exemplo: ao empurrar uma parede sentimos a “reação” da parede contra nosso esforço; mesmo ao levantar uma pena o peso dela fará uma reação contra o nosso esforço no sentido de permanecer aonde estiver... evidente que é muito mais fácil elevar uma pena do chão do que derrubar uma parede de tijolos.

3ª – A força aplicada em um corpo é diretamente proporcional à sua massa e à aceleração sentida por em determinado referencial; essa “lei” nas equações originais de Newton tem a forma:

F = dQ/dt, onde dQ é a variação da Quantidade de Movimento (Q = M.v)       e dt é a Variação de Tempo, como a Massa é invariável num sistema clássico     (v << c) então fica:

F = dQ/dt  =>  F = d M.v/dt  => (como a massa permanece constante)        F = M. dv/dt

Como dv/dt é igual a aceleração ( a ) ficamos com:

F = M.a  (Força é igual à massa vezes a aceleração)

Outros conceitos derivados da mecânica clássica newtoniana:

Energia Cinética:  EC = M.v²/2

Energia Potencial Gravitacional: EP = M . g . h (g = aceleração da gravidade – 9,8 m/seg²; h = altura do corpo em relação ao nível do mar).

Trabalho de uma força:  T = F. d. cosΦ (F – força, d – distância, cosΦ – cosseno do ângulo que a força faz em relação ao eixo horizontal do referencial).

Princípio da conservação de energia: em qualquer sistema físico a energia total se conserva ao longo do tempo; por exemplo, num corpo em queda livre toda a energia potencial gravitacional é sempre transformada em energia cinética, em qualquer ponto de sua trajetória.

Simetria, galáxias e divindades

Gluons, taquions, leptons, quarks, hadrons, gatos, humanos... somos todos o resultado de uma quebra de uma simetria (muito tênue) ocorrida num átimo de tempo antes do Big Bang.

Mas a Natureza nos deixou ainda alguns sinais, quase explícitos, desse momento onde dimensões espaço-temporais estavam tão enroladas em si mesmas, que a beleza, essa coisa que nos fascina-encanta-seduz, não podia sequer ser cogitada; vislumbramos o explendor desse instante único (pelo menos para o nosso Universo, se Hugh Everett e Bryce DeWitt estejam certos e existam outros):

Em galáxias:

 (Andrômeda ou M-31)

E em deusas:

Dica de Física 0003

Gráficos em Física - uma introdução


Para que serve um gráfico em Física?

O gráfico serve para visualizar o comportamento das grandezas físicas envolvidas de uma maneira fácil e rápida.

Através de um gráfico podemos verificar como varia uma grandeza (por exemplo, espaço) em função de outra (por exemplo, tempo).

Vamos mostrar como construir e interpretar o gráfico espaço em função do tempo como exemplo. 


Sistema de Eixos Cartesianos Ortogonais

Para construir um gráfico, utiliza-se um sistema de eixos cartesianos ortogonais que são dois eixos perpendiculares entre si, sendo o ponto de intersecção denominado origem. 

Os valores das grandezas envolvidas são colocados utilizando uma escala adequada para cada eixo.

O eixo na horizontal (por convenção) é denominado eixo das abcissas e nele são colocadas os valores da variável independente (por exemplo, tempo). 

O eixo na vertical é denominado eixo das ordenadas e nele são colocados os valores da variável dependente (por exemplo, espaço).


Localização de um ponto no plano cartesiano

O par de coordenadas (t,S) localiza a posição do ponto no plano cartesiano definido pelos eixos cartesianos. Para tal traça-se uma perpendicular do ponto ao eixo das abcissas e outra perpendicular ao eixo das ordenadas, determinando, respectivamente, a abcissa e a ordenada do ponto (fig. 1).




Figura 1 - Localizando um ponto no plano cartesiano
 
Construção de gráficos

Para construir qualquer gráfico envolvendo grandezas físicas, deve-se observar as seguintes regras:

• Coloque título e legenda.
• Escolha escalas adequadas para colocar os valores nos eixos.
• Coloque, de forma clara, as grandezas a serem representadas nos eixos com as suas respectivas unidades.
• Coloque os valores das grandezas apenas com os números necessários à leitura; não coloque valores especiais.
• Quando houver diversas séries de medidas, é conveniente distingüi-las com diferentes símbolos (, , e outros).

Procure traçar a melhor reta ou curva, devendo recorrer a métodos matemáticos quando os valores encontrados não estão adequados.

Exemplo 1 - Construção de gráficos
 
Construir um gráfico de S = f(t), espaço em função do tempo, dada a tabela abaixo.

S (m)	t (s)
0	0
5	1
10	2
15	3
20	4
25	5

Observe que o espaço (S) é a variável dependente e o tempo (t) é a variável independente, e que quando a grandeza tempo dobra, triplica ou quadruplica seu valor, a grandeza espaço (S) também dobra, triplica ou quadruplica seu valor, indicando que as grandezas espaço e tempo são diretamente proporcionais.

 

Adotar uma escala, por exemplo:

1 cm - 5 m para a variável S

1 cm - 1 s para a variável t

Figura 2 - Gráfico espaço (S) versus tempo (t)



Determinação da inclinação da reta

Observe que o gráfico S versus t da fig. 2 é uma reta passando pela origem, indicando que o espaço é uma função do 1^o. grau do tempo. A inclinação da reta é dada pelo cociente entre a diferença das ordenadas e a diferença das abcissas.

Inclinação da reta = (Sfinal - S inicial ) / ( tfinal - tinicial)

No exemplo dado, escolhendo dois pontos quaisquer sobre a reta (fig. 2), A e B, para calcular a inclinação da reta:

Inclinação da reta = ( S_B - S_A)/(t_B - t_A) = (15 - 5) m / (3 - 1) s = (10 m) / (2 s) = 5 m/s

O valor encontrado é o da velocidade, e podemos concluir que:


A velocidade de um móvel pode ser determinada a partir do gráfico S versus t (quando este for uma reta), pela inclinação da reta.

Quanto mais inclinada a reta estiver em relação ao eixo das abcissas, para uma mesma escala, maior será a velocidade e vice-versa.

Vimos o exemplo de um gráfico de uma função do 1^o grau que é uma reta.

Podemos obter diferentes tipos de gráficos tais como: parábola, hipérbole, e outros, dependendo da função matemática envolvida.

Fonte: http://educar.sc.usp.br/fisica/graficos.html

Dica de Física 0002

Instrumentos ópticos

Instrumentos de projeção

 São aqueles cuja imagem formada é real, pois pode ser projetada sobre um filme, uma tela, um anteparo, etc.    
                                    

 I- Câmera fotográfica – ou máquina fotográfica --- dispositivo utilizado para capturar imagens. Consiste básicamente de uma caixa com orifício no qual se encontram uma ou mais lentes convergentes (objetiva), por onde entram os raios de luz  provenientes dos objetos que queremos fotografar ou filmar e que produzem uma imagem real, menor e invertida sobre o filme (câmera comum) ou sobre um censor que armazena as imagens em cartões de memória (câmera digital).

           

     

 

 Quando queremos focalizar a imagem devemos variar a distância lente-filme ou seja, variar P’ pois P e o foco são constantes. Assim, quando o objeto se aproxima devemos afastar a lente para que a imagem seja projetada novamente sobrfe o filme. 

 II- Projetor – Consta de uma fonte de luz que, através de uma intensa iluminação e de uma lente convergente (ou um sistema de lentes), projeta a imagem de um objeto (filme, slide, transparência) em uma tela. Essa imagem é real, invertida e maior, desde que o objeto esteja entre A e F.

                      

     

Instrumentos de observação

 A imagem é observada diretamente pelo observador e é virtual e direita.

 I-Lupa – Também chamada de lente de aumento é uma simples lente convergente que fornece de um objeto colocado entre seu foco F e seu centro óptico O uma imagem virtual, direita e maior que o objeto observado.

           

Observe no esquema abaixo a formação da imagem A’B’ de um objeto AB em uma lupa

Observe que a imagem é virtual e assim, nas equações 1/f = 1/P + 1/P’, i/o = -P’/P e A = i/o = -P’/P, P’ deve e ser substituída com sinal negativo, pois P’< 0.

 II- Microscópio composto- Utilizado na observação de regiões de dimensões microscópicas que o olho humano não consegue perceber, como por exemplo, na histologia, anatomia, mineralogia, etc.

  

Consta de duas lentes convergentes (geralmente compostas) de pequenas distâncias focais que são: a objetiva (sistema de lentes bastante sofisticado) que está próxima ao objeto observado e a ocular (com no mínimo duas lentes) com a qual observamos a imagem fornecida pela objetiva.

Veja o esquema simplificado do microscópio composto.

A distância focal da objetiva é muito pequena (milímetros). A objetiva forma do objeto AB uma imagem A’B’ real, invertida e maior que o objeto e essa imagem serve como objeto para a ocular (de distância focal da ordem de centímetros) que fornece uma imagem final A’’B’’, virtual, maior e direita em relação a A’B’. Observe que A’’B’’ é direita em relação a A’B’ e invertida em relação ao objeto AB.

O aumento linear transversal do microscópio é fornecido pela expressão:

A_microscópio= A_objetiva . A_ocular

O aumento produzido por esse microscópio chega até a 2000 vezes. Atualmente existem microscópios eletrônicos que produzem ampliações de até cem mil vezes.

 III- Luneta astronômica – utilizada na observação de astros ou de objetos distantes.

     

Consta de 2 lentes convergentes, a objetiva e a ocular.  Ao contrário do microscópio composto, a distância focal da objetiva é muito grande (da ordem de metros). A ocular tem pequena distância focal.

Devido ao fato de o objeto estar muito afastado, a imagem (i1) formada pela objetiva está praticamente sobre seu foco (Fobj) e é real e invertida (veja figura).

                           

Essa imagem (i₁) vai servir como objeto para a ocular resultando numa imagem final (i₂), virtual e invertida em relação ao objeto. Observe que os focos da ocular (F_oc) e da objetiva (F_obj) estão muito próximos, praticamente coincidindo.

O aumento desta luneta é dado por  A=f_obj / f_oc. Observe por essa expressão que, para que o aumento seja bem grande, a distância focal da ocular deve ser bem menor que a da objetiva, ou seja, f_oc < f_ob.       

No caso de uma luneta terrestre, onde a imagem final não é invertida devemos trocar a lente ocular convergente por uma lente divergente que tem distância focal negativa. Como o aumento é dado por A=f_obj / f_oc, é claro que maior será o aumento quanto maior o módulo da objetiva for maior que o módulo da ocular.

Fonte: http://www.fisicaevestibular.com.br/optica15.htm

Dica de Física 0001

Lentes - Construção geométrica de imagens

 Lente - Dispositivo feito de material homogêneo e transparente no qual uma das superfícies é plana e a outra esférica ou as duas superfícies são esféricas.

Serão chamadas lentes delgadas quando sua espessura for desprezível em relação ao seu raio de curvatura que é o raio da(s) circunferências que as geraram..       

        

  São:

côncavo-convexa      biconvexa     plano-convexa

R_côncavo>R_convexo      R_plano>R_convexo   

Convexo-côncava     bicôncava     plano-côncava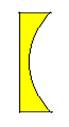

R_convexa>R_côncava       R_plana>R_côncava

  Como normalmente temos lentes de vidro imersas no ar, então, neste caso, as lentes de bordas (extremidades) finas são lentes convergentes e lentes de extremidades grossas são lentes divergentes.

  Costumamos representar lente delgada (espessura desprezível quando comparada com seu raio de curvatura):

lentes convergentes      lentes divergentes

Elementos de uma lente:

  Centro óptico O – ponto onde o eixo principal (ep) corta a lente (convergente ou divergente). É sempre válida a seguinte propriedade:

Todo raio de luz que passa pela lente pelo seu centro óptico (O) não sofre desvio.

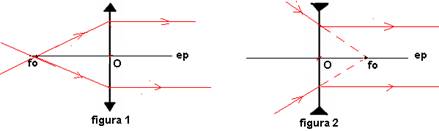
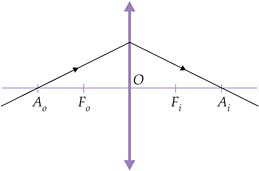
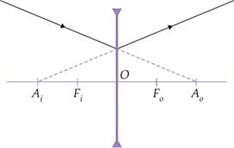
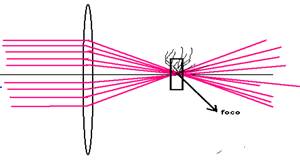
   Foco principal objeto f_o  - por ele passam os raios incidentes na lente convergente (figura 1) ou seus prolongamentos na lente divergente (figura 2).

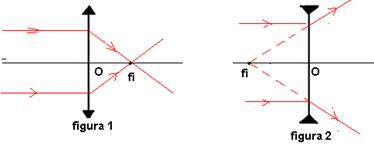
  Foco principal imagem f_i  - por ele passam os raios que emergem na lente convergente quando nela os raios incidem paralelamente ao eixo principal (figura 1) e por ele passam os prolongamentos dos raios emergentes quando na lente divergente incide um feixe de raios paralelos. (figura 2).

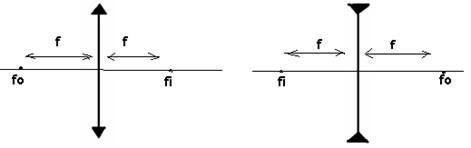
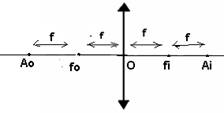
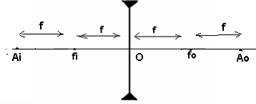
   Distância focal da lente f – corresponde à distância de f_o a O ou de f_i a O, para as duas lentes (convergentes e divergentes).

   Ponto antiprincipal objeto A_o e imagem A_i  - são pontos cuja distância ao centro óptico O da lente é o dobro da distância focal.  

      

  Raios notáveis

   Todo raio de luz que incide na lente passando pelo foco objeto emerge paralelamente ao eixo principal (convergente) e todo raio de luz que incide na lente de modo que seu prolongamento passe pelo foco objeto emerge paralelamente ao eixo principal (divergente).

      

   Todo raio de luz que incide paralelamente ao eixo principal é refratado passando (ou seu prolongamento) pelo foco imagem.

       

   Todo raio de luz que incide paralelamente ao eixo principal é refratado passando (ou seu prolongamento) pelo foco imagem.

       

   Todo raio de luz que incide passando pelo centro óptico da lente não sofre desvio ao se refratar.

       

   Todo raio de luz que incide na lente passando pelo ponto antiprincipal (objeto ou imagem) se refrata passando pelo ponto antiprincipal (imagem ou objeto).

       

  

  Construção geométrica de imagens:

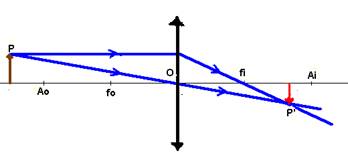
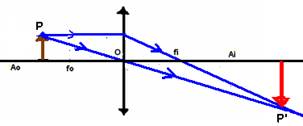
Lente convergente

1^o caso: Objeto P antes de A_o

                                        

Características da imagem P’:

Natureza – Real (obtida no cruzamento do próprio raio luminoso (linha cheia)

Localização – entre F_i e A_i  

Tamanho e orientação – menor que o objeto e invertida em relação ao mesmo

Utilidades

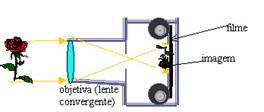
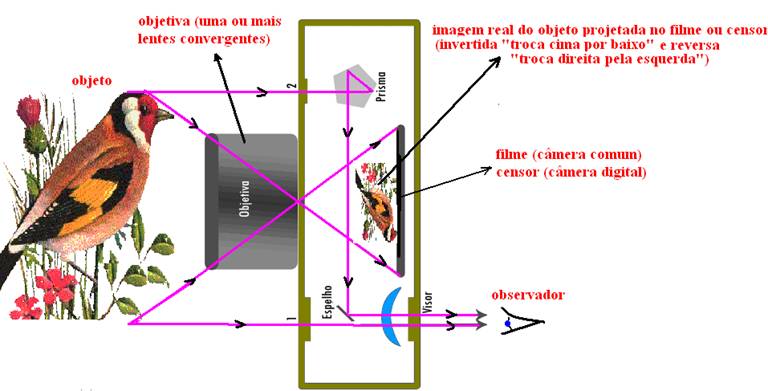
-- Uma máquina fotográfica e uma filmadora tem seu sistema óptico como nesse caso onde a imagem formada no filme é real, invertida e menor.

-- O mesmo acontece numa máquina de xérox quando queremos reduzir um documento.

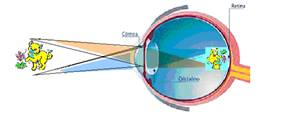
-- O globo ocular funciona também de modo semelhante, pois seus vários componentes transparentes funcionam como

uma lente convergente formando na retina uma imagem real, menor e invertida.

2^o caso: Objeto P sobre A_o

Características da imagem P’:

Natureza – real

Localização – sob A_i

Tamanho e orientação – mesmo tamanho que o do objeto e invertida em relação a ele.

Utilidade: Xérox – tamanho normal

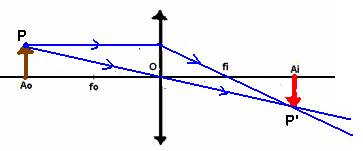
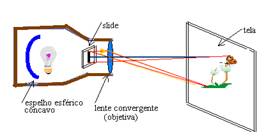
3^o caso: Objeto entre A_o e f_o

Natureza: - real

Localização – Depois de A_i

Tamanho e orientação – maior que o objeto e invertida em relação a ele.

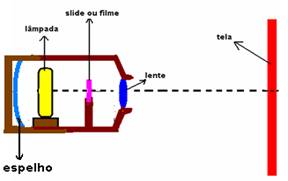
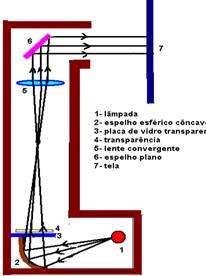
Utilidades – projetores de filmes e de slides que fornecem do filme ou slide (objetos) uma imagem real, invertida e maior, projetada numa tela.

    

- xérox – ampliação

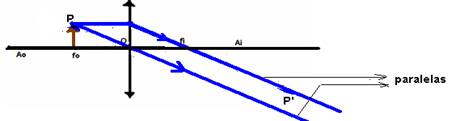
4^o caso:Objeto sobre o foco f_o

Neste caso dizemos que a imagem é imprópria (está no infinito).

Aplicação – geração de feixes de raios paralelos, microscópios, etc.

5^o caso:Objeto entre f_o e O

Natureza: Virtual (obtida no cruzamento dos prolongamentos dos raios luminosos.

Localização: Antes de f_o

Tamanho e orientação: Maior que o objeto e direita em relação a ele.

Utilidade – Lupa (lente de aumento) e microscópios.

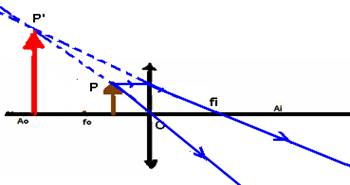
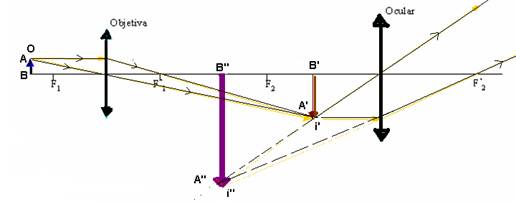
Lente divergente

Neste caso, independente da posição do objeto, a imagem  P’será sempre:   

   

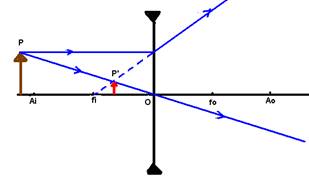
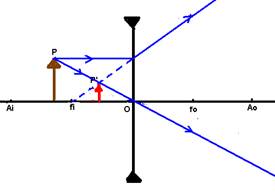
Natureza – virtual

Localização  - entre O e f_i

Tamanho e orientação – menor que o objeto e direita em relação a ele.

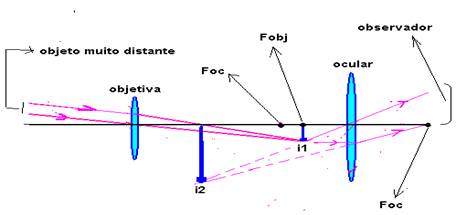
Aplicação – correção de miopia, oculares em microscópios, lunetas e binóculos.

                                                                             

O que você deve saber

   Toda imagem virtual é direita e toda imagem real é invertida.
   Toda imagem real pode ser projetada numa tela, ser filmada, fotografada, etc.

   Entre o objeto e a imagem, o elemento que se encontra mais afastado da lente tem maior tamanho.

  Guarde apenas que a imagem fornecida por uma lente divergente é sempre virtual, direita e menor que o objeto. Para qualquer outro tipo de imagem, a lente é convergente.

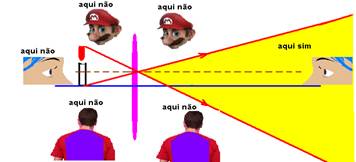
   Para que você consiga ver uma imagem de um objeto, através de uma lente é preciso que você se coloque numa posição em que os raios de luz que emergem da lente atinjam os seus olhos.

   Não é possível queimar papel com uma lente divergente, somente com lente convergente pois os raios efetivos de luz (não seus prolongamentos) provenientes do sol devem convergir para o papel.

   Se uma lente quebrar, cada caco funciona como uma lente semelhante à inteira, com a mesma distância focal, pois os raios de curvatura de cada face permanecem os mesmos e fornecem imagem com as mesmas características da inteira, apenas com menor brilho, pois a quantidade dos raios de luz recebidos é menor.

  Lentes de bordas (extremidades) delgadas (finas) -  se n_lente>n_meio, a lente é convergente como, por exemplo, lentes de vidro no ar  e caso contrário, divergente, como, por exemplo, lentes de ar no vidro.

  Lentes de bordas (extremidades) espessas (grossas) – se  n_lente>n_meio,a lente é divergente, como por exemplo, lentes de vidro no ar e caso contrário, convergente, como por exemplo lentes de ar no vidro.

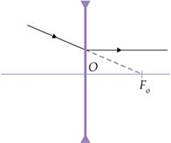
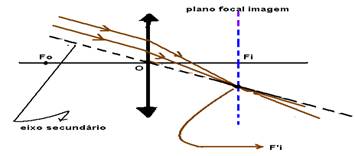
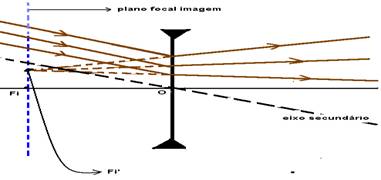
  O plano focal secundário de uma lente é o plano frontal que passa pelo foco principal. Assim, quando um feixe de raios paralelos incide numa lente convergente, paralelamente a um de seus eixos secundários, se refrata convergindo em um ponto F_i’ que pertence ao plano focal secundário imagem dessa lente.

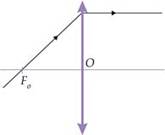
Analogamente, se a lente for divergente, teremos:

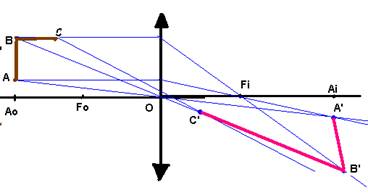
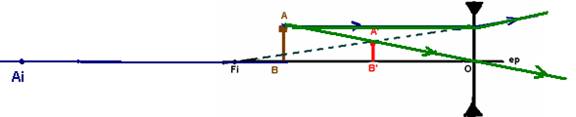
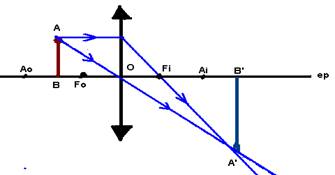
   Para determinar a imagem A’B’C’ de um corpo extenso ABC você deve localizar a imagem de cada ponto e depois uni-las. Exemplo:

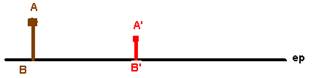
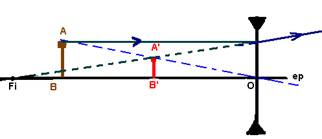
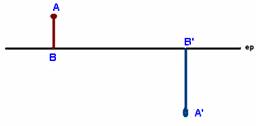
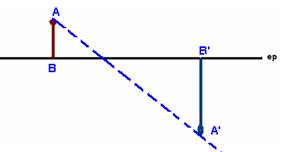
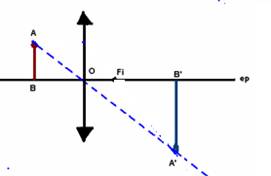
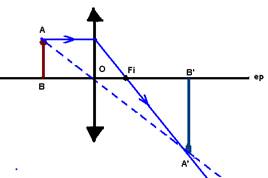
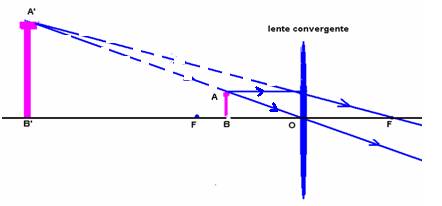
   Dados um objeto AB, sua imagem A’B’ e o eixo principal de uma lente, localizar a lente, seu foco F, seu ponto anti-principal  e esquematizar dois raios de luz que determinam a imagem

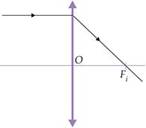
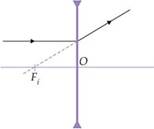
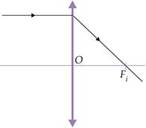
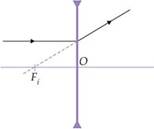
Etapas:

1^a- Identificar a lente – é divergente pois a imagem é direita e menor que o objeto.

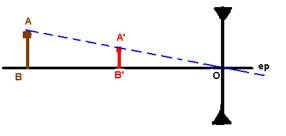
2^a- Traçar uma reta que, passando por A e A’ irá interceptar o ep e neste ponto está o eixo óptico da lente.

3^a- A partir de A, traçar um raio de luz que, incidindo paralelamente ao eixo principal sofra refração na lente, divergindo, de modo que seu prolongamento passe por A’ e intercepte o ep no foco F_i.

4^a- A distância de A_i a O é o dobro da distância de F_i a O. Os raios de luz que determinam a imagem são os raios 1 e 2 da figura abaixo.

Lembre-se de que F_o e A_o são simétricos e estão do outro lado da lente.

-Se a lente for convergente, as etapas são as mesmas.

 Exemplo:

1^a – Lente convergente – a imagem é maior que o objeto e é invertida

2^a = Unir A com A’ e localizar a lente.

     

3^a – Traçar um raio de luz que, partindo de A, intercepte o ep no F_i e passe por A’.

4^a – Localizar A_i tal que OF_i=F_iA_i  e lembrar que F_o e A_o são simétricos a F_i e A_i e traçar os dois raios de luz que determinam a imagem.

 

Links úteis:

http://www.if.usp.br/gref/optica/optica3.pdf

http://educar.sc.usp.br/otica/instrume.htm

http://www.colmagno.com.br/plus3/fisica/fisi_ppt12.ppt

http://pt.wikipedia.org/wiki/Instrumento_%C3%B3ptico

http://www.passeiweb.com/na_ponta_lingua/sala_de_aula/fisica/optica/optica/lentes

http://www.fisicaevestibular.com.br/optica12.htm